Actividad 7 - Grafos

Actividad:

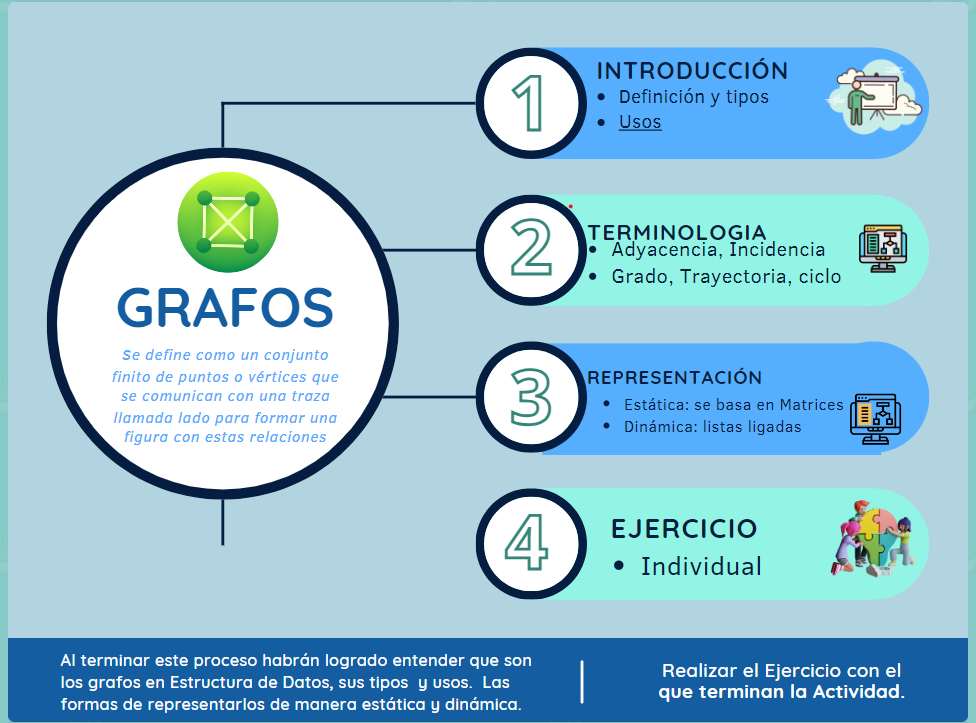
1. Definir que es un grafo

2. ¿Que uso se le dan a los grafos?

3. ¿Como se pueden clasificar los grafos?

4. ¿Como se pueden representar los grafos?

Nota: Recuerde que cada pregunta debe ir acompañada de:

• Los enlaces de donde consulto la información (normas Apa) .
• De un aporte personal con sus propias palabras de lo que entendió de lo consultado.
• De una imagen que tenga relación con el tema o pregunta con su respectivo enlace (normas Apa)
• Insertar un video video (youtube) que explique o aclare la pregunta con su enlace respectivo (normas Apa)
• Debajo del video realizar un resumen de lo que dice o explica el autor del video.

1. Definir qué es un grafo

Definición: Un grafo es una estructura matemática que consta de un conjunto de vértices (nodos) y un conjunto de aristas (edges) que conectan pares de vértices. Los grafos se utilizan para modelar relaciones y conexiones entre diferentes entidades.

Fuente consultada: Gross, J. L., & Yellen, J. (2006). Graph Theory and Its Applications. CRC Press.

Aporte: Entiendo que un grafo es una herramienta esencial en matemáticas y ciencias de la computación que permite representar y analizar relaciones complejas entre objetos de manera gráfica y estructurada.

Fuente: Wikimedia Commons

Video explicativo: Graph Theory Basics - Graphs and Edges

Resumen del video: El video explica los conceptos básicos de la teoría de grafos, incluyendo la definición de vértices y aristas, y muestra ejemplos de grafos no dirigidos y dirigidos, así como la importancia de los grafos en la representación de redes y relaciones.

2. ¿Qué uso se le dan a los grafos?

Usos de los grafos:

1. Redes sociales: Modelar relaciones entre usuarios.
2. Rutas de transporte: Optimización de rutas y mapas.
3. Circuitos electrónicos: Diseño y análisis de circuitos.
4. Bases de datos: Representación de relaciones entre datos.

Fuente consultada: Diestel, R. (2005). Graph Theory. Springer-Verlag.

Aporte: Los grafos son increíblemente versátiles y se aplican en diversos campos para resolver problemas de conexión, optimización y análisis de estructuras complejas, desde redes sociales hasta ingeniería de sistemas.

Fuente: Wikimedia Commons

Video explicativo: Applications of Graph Theory

Resumen del video: El video describe varias aplicaciones prácticas de la teoría de grafos, destacando su uso en la modelación de redes sociales, rutas de transporte, y la resolución de problemas como el del viajante y el de los colores de grafos.

3. ¿Cómo se pueden clasificar los grafos?

Clasificación de grafos:

1. Grafo no dirigido: Las aristas no tienen dirección.
2. Grafo dirigido: Las aristas tienen una dirección.
3. Grafo ponderado: Las aristas tienen un peso asociado.
4. Grafo no ponderado: Las aristas no tienen peso.

Fuente consultada: Bondy, J. A., & Murty, U. S. R. (2008). Graph Theory. Springer.

Aporte: Comprender la clasificación de los grafos permite seleccionar el tipo adecuado para cada aplicación, dependiendo de si se necesita representar relaciones bidireccionales, direccionales, o con diferentes costos.

Fuente: Wikimedia Commons

Video explicativo: Types of Graphs in Graph Theory

Resumen del video: El video presenta diferentes tipos de grafos, explicando las características distintivas de grafos dirigidos, no dirigidos, ponderados y no ponderados, y su aplicabilidad en diferentes contextos.

4. ¿Cómo se pueden representar los grafos?

Representaciones de grafos:

1. Lista de adyacencia: Cada vértice tiene una lista de vértices adyacentes.
2. Matriz de adyacencia: Una matriz donde las filas y columnas representan vértices y las entradas indican la presencia de aristas.
3. Lista de aristas: Una lista de pares que representan las aristas del grafo.

Fuente consultada: West, D. B. (2001). Introduction to Graph Theory. Prentice Hall.

Aporte: La representación de un grafo depende de las necesidades específicas del problema a resolver; por ejemplo, listas de adyacencia son eficientes en espacio para grafos dispersos, mientras que matrices de adyacencia permiten acceso rápido para grafos densos.

Fuente: Wikimedia Commons

Video explicativo: Graph Representations: Adjacency Matrix and Adjacency List

Resumen del video: El video explica cómo representar grafos utilizando matrices de adyacencia y listas de adyacencia, describiendo las ventajas y desventajas de cada método, y proporcionando ejemplos claros para ilustrar ambos enfoques.

Contesta las siguientes preguntas dando una explicación corta:

1. Qué relación hay entre la estructura árbol y la estructura grafo? Puede ser un grafo un árbol?
2. Es un grafo una estructura recursiva? Explique
3. Para qué tipo de problemas se utiliza la estructura grafo? De dos ejemplos
4. Como se puede representar la estructura grafo? Explique
5. Construya dos grafos: Uno dirigido y otro no dirigido

1: Los árboles son un tipo especial de grafo que no contiene ciclos y está conectado. Cada árbol puede considerarse como un grafo, pero no todos los grafos son árboles. Los árboles son simplemente un caso particular de grafos que cumplen con ciertas propiedades específicas, como la ausencia de ciclos y la conectividad.

2: Sí, un grafo puede ser considerado una estructura recursiva en la medida en que la recursión se utiliza para representar y explorar los nodos y aristas del grafo.

3: La estructura de grafo es ampliamente utilizada para resolver una variedad de problemas en campos como la informática, las matemáticas, la ingeniería y más. Aquí tienes dos ejemplos comunes de problemas para los cuales se utiliza la estructura de grafo:

Rutas y Conectividad: Problemas que implican encontrar rutas más cortas entre puntos o determinar la conectividad entre elementos. Por ejemplo:

1. • Problema del camino más corto: Encontrar la ruta más corta entre dos ubicaciones en una red de carreteras o en una red de computadoras.
   • Conectividad en redes sociales: Determinar si dos personas están conectadas a través de una cadena de amistades en una red social.

2. Planificación y Asignación de Recursos: Problemas que implican la asignación eficiente de recursos o la planificación de actividades. Por ejemplo:

• Asignación de tareas: Asignar tareas a trabajadores de manera que se minimice el tiempo total de ejecución o se maximice la eficiencia.
• Planificación de rutas de transporte: Planificar rutas de transporte público para minimizar el tiempo de viaje total o maximizar la cobertura de áreas.
  

4: 

Un grafo es una estructura de datos que consiste en un conjunto de vértices (o nodos) y un conjunto de aristas (o edges) que conectan pares de vértices. Se puede clasificar en:

1. Grafo no dirigido: Las aristas no tienen dirección, y la relación entre los vértices es bidireccional.
2. Grafo dirigido: Las aristas tienen una dirección, indicando una relación unidireccional entre los vértices.
3. Grafo ponderado: Las aristas tienen pesos asociados que pueden representar costos, distancias u otras medidas.
4. Grafo no ponderado: Las aristas solo indican la conexión entre los vértices, sin ningún peso asociado.

Los grafos se pueden representar principalmente de tres maneras:

1. Lista de Adyacencia: Cada vértice tiene una lista de vértices adyacentes.

   • Ventajas: Eficiente en términos de espacio para grafos dispersos (sparse).
   • Desventajas: Puede ser menos eficiente para verificar si existe una arista entre dos vértices.

2. Matriz de Adyacencia: Es una matriz cuadrada donde las filas y columnas representan vértices. La entrada en la posición (𝑖,𝑗)(i,j) indica la presencia (y, opcionalmente, el peso) de una arista entre los vértices 𝑖i y 𝑗j.

   • Ventajas: Rápida para verificar la existencia de una arista entre dos vértices.
   • Desventajas: Consume más espacio, especialmente para grafos dispersos.

3. Lista de Aristas: Es una lista de pares (o tuplas) que representan las aristas del grafo.

   • Ventajas: Sencilla y directa, útil para grafos densos y para listar todas las aristas.
   • Desventajas: No es eficiente para operaciones de adyacencia y búsqueda de vértices conectados.

Actividad de lista ligada de adyacencia para el los grafos Y y Z