Actividad 6 - Árboles

1.1Arboles generales y su representación

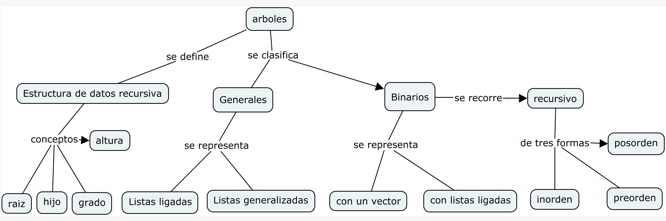
La definición de árboles parte del concepto de árbol general que no incluye el árbol sin ningún registro. Además se definen los conceptos básicos asociados a los árboles.

1.1.1Definición de Arboles generales

Un árbol es un conjunto de n registros(n>0), donde el árbol vacío no está definido, de tal manera que hay un registro llamado raíz y los otros registros están partidos en conjuntos disjuntos cada uno de los cuales tiene las mismas características de la definición del árbol (esta característica hace comportar la estructura árbol como recursiva).

1.1.2 Terminología de arboles

l. Las ramificaciones de cada nodo se les denomina hijos y los nodos desde donde parten las ramificaciones se denominan padres. Los registros con el mismo padre se denominan hermanos.

• Al número de ramificaciones que tiene un registro se le denomina el grado de un registro
• El grado de un árbol se determina encontrando el registro con el más grande número de ramificaciones.
• Los registros que no tienen hijos dentro del árbol se denominan hojas. Para calcular el número de hojas de un árbol ver el video en YouTube:

Calcular las Hojas en un Árbol N-ario. (2014, 27 enero). [Vídeo]. YouTube. https://www.youtube.com/watch?v=P1G9imv8Su4

Presentación con las definiciones

Pruebas de escritorio

Actividad 6 

       Arboles Binarios Presentación con las definiciones

Documentación: 

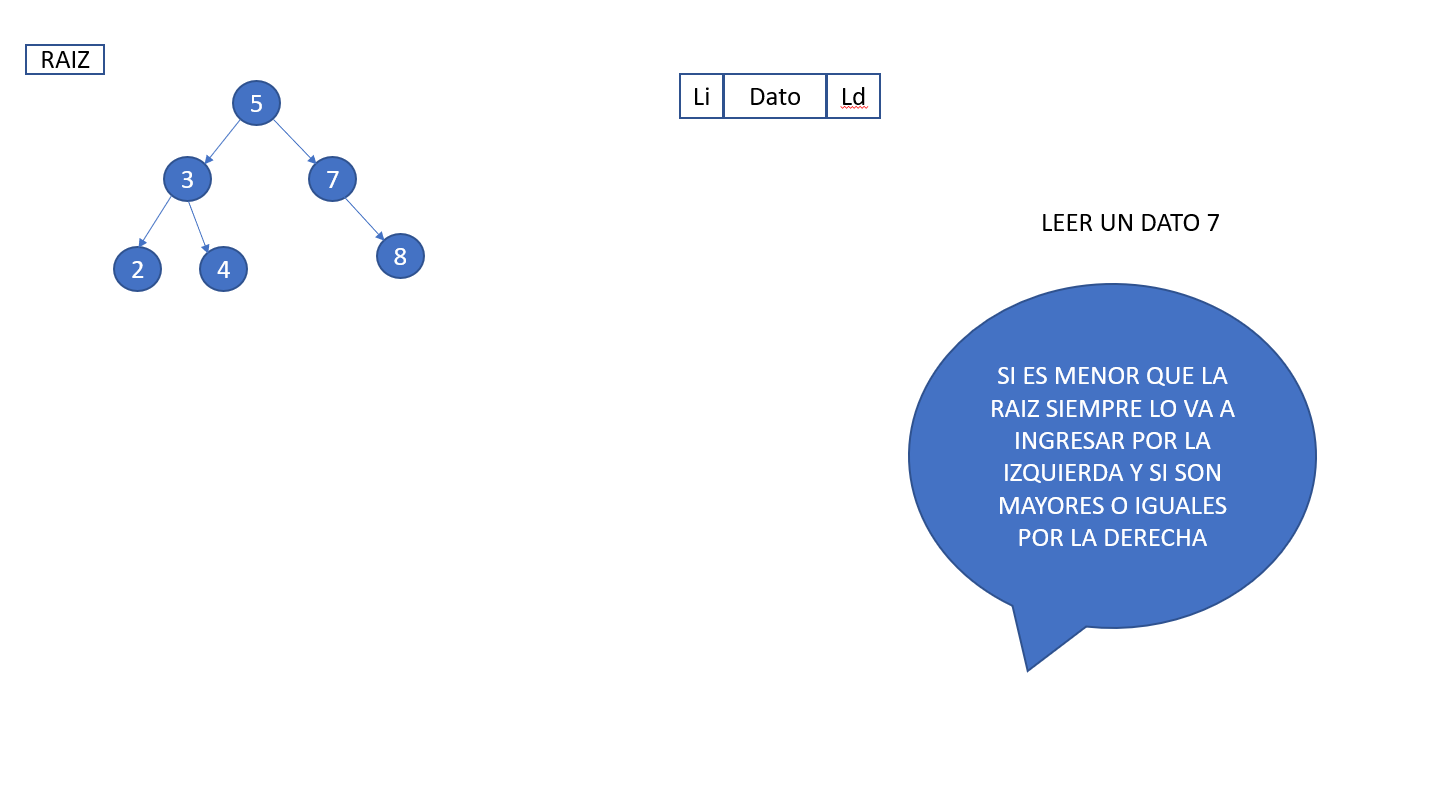
Clase Nodo:

• Atributos:

  • dato: Almacena el valor del nodo.
  • li: Referencia al hijo izquierdo del nodo.
  • ld: Referencia al hijo derecho del nodo.

• Métodos:

  • __init__(self, dato): Constructor de la clase Nodo que inicializa el valor del nodo y establece las referencias a los hijos izquierdo y derecho como None.

Clase Arbol:

• Atributos:

  • raiz: Referencia al nodo raíz del árbol.

• Métodos:

  • __init__(self, d): Constructor de la clase Arbol que crea un árbol con una raíz que tiene el valor d.
  • agrego(self, d): Método que agrega un nuevo nodo con el valor d al árbol.
  • agregar(self, nodo, d): Método auxiliar recursivo que agrega un nuevo nodo con el valor d al árbol, comparando el valor d con el valor del nodo actual y decidiendo si agregarlo como hijo izquierdo o derecho.
  • inordeno(self): Método que realiza un recorrido en orden (inorden) del árbol e imprime los valores de los nodos.
  • inorden(self, nodo): Método auxiliar recursivo que realiza un recorrido en orden del subárbol con raíz en el nodo dado e imprime los valores de los nodos en orden ascendente.
  • preordeno(self): Método que realiza un recorrido en preorden del árbol e imprime los valores de los nodos.
  • preorden(self, nodo): Método auxiliar recursivo que realiza un recorrido en preorden del subárbol con raíz en el nodo dado e imprime los valores de los nodos.
  • postordeno(self): Método que realiza un recorrido en postorden del árbol e imprime los valores de los nodos.
  • postorden(self, nodo): Método auxiliar recursivo que realiza un recorrido en postorden del subárbol con raíz en el nodo dado e imprime los valores de los nodos.
  • buscar(self, nodo, d): Método auxiliar recursivo que busca un valor d en el subárbol con raíz en el nodo dado y devuelve el nodo que contiene ese valor, si existe.
  • busco(self, d): Método que busca un valor d en el árbol y devuelve el nodo que contiene ese valor, si existe.

Programa Principal:

• Solicita al usuario ingresar un número para inicializar la raíz del árbol.
• Presenta un menú interactivo que permite al usuario realizar varias operaciones en el árbol:
  • Agregar nodos al árbol.
  • Realizar recorridos en profundidad (inorden, preorden y postorden) e imprimir los valores de los nodos.
  • Buscar un valor en el árbol.
  • Salir del programa.